Elliptical
From the Quicksilver Metaweb.
In mathematics, an ellipse is a figure resembling a circle which has been stretched in one direction. This is an example of a conic section and can be defined as the locus of all points, in a plane, which have the same sum of distances from two given fixed points (called foci, plural of focus). According to Kepler's laws, the orbit of a planet is an ellipse with the Sun at one of the foci.
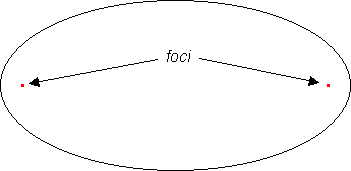
If the two foci coincide, then the ellipse becomes a circle; such an ellipse is the roundest possible ellipse; and may arguably no longer be a "true" ellipse. The eccentricity of an ellipse is greater than zero]] and smaller than one.
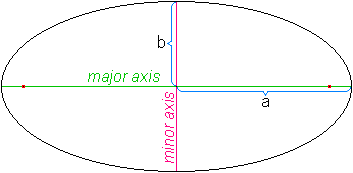
The line which passes through the foci is the major axis and also the longest line which passes through the ellipse. The line which passes through the centre (halfway between the foci), at right angles to the major axis, is the minor axis. The semimajor axis is one half the major axis; running from the center, through a focus, and to the edge of the ellipse. Likewise, the semiminor axis is one half the minor axis. The two axes are the elliptic equivalants of the diameter, while the two semiaxes are the elliptic equivalents of the radius.
The size and shape of an ellipse are determined by two constants, conventionally denoted a and b. The constant a equals the length of the semimajor axis; The constant b equals the length of the semiminor axis.
An ellipse centred at the origin of an x-y coordinate system with its major axis along the x-axis is defined by the equation
The same ellipse is also represented by the parametric equations:
which use the trigonometric functions sine and cosine.
The shape of an ellipse is usually expressed by a number called the eccentricity of the ellipse, conventionally denoted e (not to be confused with the mathematical constant e). The eccentricity is related to a and b by the statement
The eccentricity is a positive number less than 1, or 0 in the case of a circle. The greater the eccentricity is, the larger the ratio of a to b is, and therefore the more elongated the ellipse is. The ellipse shown in the image below has an eccentricity of approximately 0.88. The distance between the foci is 2ae.
The semi-latus rectum of an ellipse, usually denoted l (a lowercase L), is the distance from a focus of the ellipse to the ellipse itself, measured along a line perpendicular to the major axis. It is related to a and b by the formula al = b2.
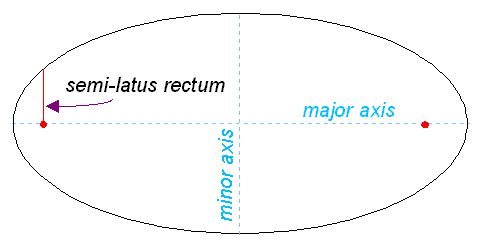
In polar coordinates, an ellipse with one focus at the origin and the other on the negative x-axis is given by the equation r(1 + ecosθ) = l
An ellipse can also be thought of as a projection of a circle: a circle on a plane at angle φ to the horizontal projected vertically onto a horizontal plane gives an ellipse of eccentricity sin φ, provided φ is not 90°.
The area enclosed by an ellipse is πab, where π is Archimedes constant. The circumference of an ellipse is 4aE(e), where the function E is the complete elliptic integral of the second kind.
Related entries
External Links
- Ellipsoid, a higher dimensional analog of an ellipse
- Spheroid, the ellipsoids obtained by rotating an ellipse about its major or minor axis.
- Super ellipse, a generalization of an ellipse that can look more rectangular